Math – Formula Layouts
Using Brackets in Formulas
The most difficult part in using LibreOffice Math is when writing complicated formulas. This is because LibreOffice Math knows nothing about the order of operations. We need to use brackets in order to state the order of operations explicitly. Consider the example which has been shown in the below given illustration.
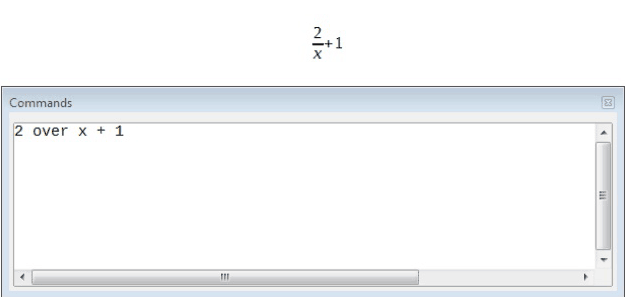 Now consider the one shown below:
Now consider the one shown below:
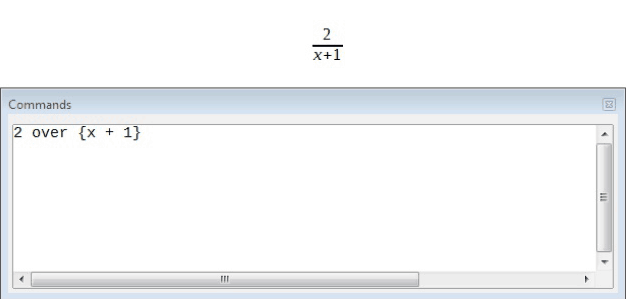 These two examples make it perfectly clear as to how the order of operations needs to be set using brackets. The use of brackets changes the formula completely.
These two examples make it perfectly clear as to how the order of operations needs to be set using brackets. The use of brackets changes the formula completely.
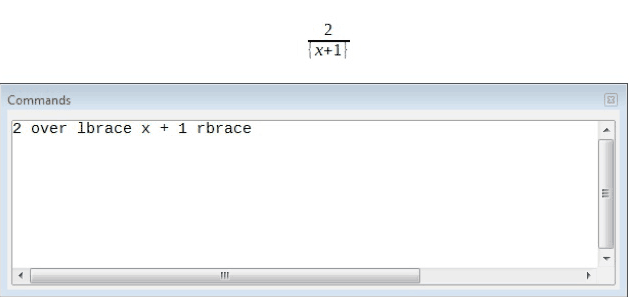
The brackets belong solely to the layout of the markup code and are not printed. If you wish to print the brackets in the formula, you need to use the commands, ‘lbrace’ and ‘rbrace’. The usage has been shown in the below given illustration.
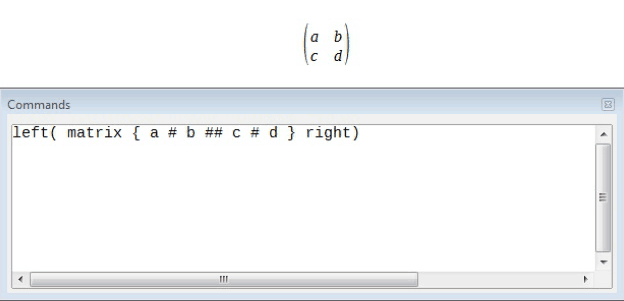
 LibreOffice Math also provides scalable brackets. This means that the brackets grow in size to match the size of the contents. We can use the commands left (and right) to make scalable brackets.
LibreOffice Math also provides scalable brackets. This means that the brackets grow in size to match the size of the contents. We can use the commands left (and right) to make scalable brackets.
Before using scalable brackets, let us see what happens when properly scaled brackets are not used. For this we need to write a matrix. A matrix has been written in the below given illustration. Rows are separated by two ‘#’s and entries within each row are separated by one ‘#’.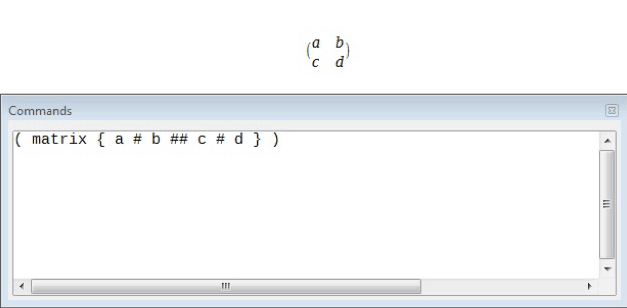
As can be seen, the brackets are not properly scaled. Now when we use the left and right commands, properly scaled brackets will get printed.
 One important point which needs to be always considered is that Math expects that for every opening bracket there will be a closing one. If you forget a bracket, Math places an inverted question mark by the corresponding bracket. The inverted question mark disappears when all the brackets are matched. Sometimes forgetting a bracket causes the whole structure of the formula to fall apart.
One important point which needs to be always considered is that Math expects that for every opening bracket there will be a closing one. If you forget a bracket, Math places an inverted question mark by the corresponding bracket. The inverted question mark disappears when all the brackets are matched. Sometimes forgetting a bracket causes the whole structure of the formula to fall apart.
However, an unpaired bracket is sometimes necessary. In such cases, we have two options. With non-scalable brackets, we need to use a preceding backslash ‘\’ to indicate that the following character should not be regarded as a bracket but as a literal character. So the half-open interval ‘[a;b[’ is represented by ‘\[ a;b \[’.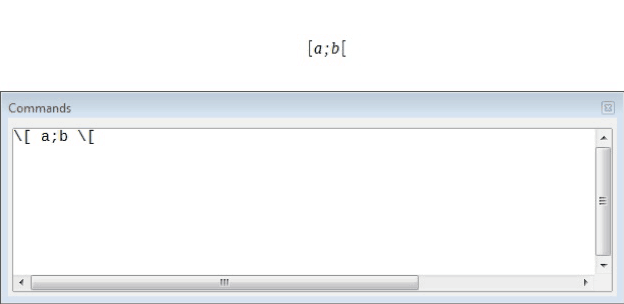
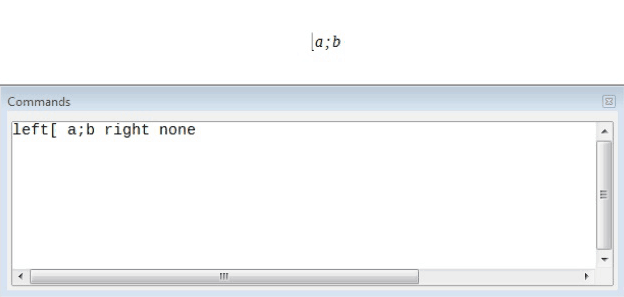
Scalable brackets can also be unpaired. The same half-open interval is represented by ‘left[ a;b right[’.
For scalable brackets, you can also use the command ‘none’ to replace a non-existent paired bracket.